Minimal cover problems and the live Phish repertoire

TL;DR

For the impatient who just want the answer, working with the static data I found on github which spans October 23, 1984 to January 15, 2017, we can generate two answers. The minimum number of shows to see all Phish original songs over that period is 70 shows. The minimum number of shows to see all Phish originals plus covers over that same time period is 246 shows. If one had the full data set up to the current date, it would be easy to re-run the analysis and determine a minimal cover.

Now – how did I calculate that? Read on.

A challenging algorithmic problem

A naïve approach to solving the problem rapidly shows that it’s not a trivial problem. In fact, it turns out to be an instance of the minimum set cover problem, one of the canonical examples of an NP-complete problem. For those unfamiliar with algorithm analysis and theoretical computer science, in very hand-wavy terms NP-complete problems are very hard problems to solve since “efficient” algorithms are unknown for them. As you increase the amount of data to consider, an algorithm to solve the problem takes significantly longer as the data set grows. This becomes apparent if you try a greedy approach or even a clever heuristic: while you may be able to find a cover for all of the songs, finding one that is minimal turns out to be quite time consuming. So much so that you’ll likely run out of patience during the search process and start googling for a better solution.

The set cover problem

Stepping back to look at the problem I mentioned above, we should look at what a set cover is and what it means for one to be minimal. The set cover problem can be summarized as follows. Say we have a set, S, of items - in this case, songs.

S = {A,B,C,D,E}

Here we have five songs (A,B,C,D,E). We also have another set, H, of shows where each member of H is a subset of the big set of songs: here, each subset corresponds to a show containing a handful of songs.

H = { {A,B}, {D,E}, {C,D,E}, {A,C,E}, {E}, {C} }

The graphic above illustrates how these are related: for each song and show, there is an edge between them showing that they are related. Finding a set cover entails finding a subset H’ of H such that the union of the members of this subset is equal to S itself. For example:

H’ = {{A,B}, {D,E}, {E}, {C}}

This set H’ a cover for the set S containing four members of H. Careful examination of H though shows that a smaller collection of shows is also a cover, and happens to be the smallest such one that can be found:

H’ = {{A,B}, {C,D,E}}

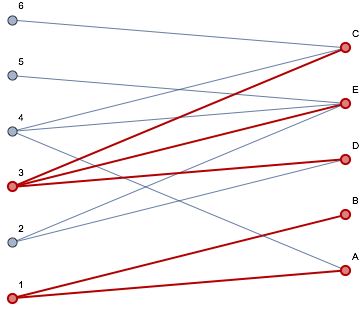
Finding some set H’ is actually not too hard with a greedy algorithm: pick any member of H, add it to H’. Determine the remaining members of S that are not a part of any set in H’. Find any member of H that contains at least one of those, and repeat until no more members of S remain to be found. The issue is that such an algorithm, while it yields a set cover for S, doesn’t guarantee that the cover will be minimal. For the Phish setlist data, we can see that the data is much more complex - there are LOTS of edges between the shows on the left and the songs on the right. By the way, don’t read anything into any patterns you think that you see in this visualization - the ordering of vertices on both sides is arbitrary.

How do we tackle solving this set cover problem for the larger setlist data? It turns out NP-complete problems like this come up all over the place in operations research, software verification, and a ton of other places. As such, a number of tools have been created that provide very fast methods to solve certain problems that are in that complexity class. I am using just one type of tool here to solve the problem: many others exist, especially if you start digging around through the tools that are out there in the field of operations research and optimal scheduling.

Satisfiability Modulo Theories

The class of tool that I use here is known as a Satisfiability Modulo Theories (SMT) solver. These are related to programs that solve another problem that is NP-complete: the Boolean satisfiability problem. Those solvers, known as SAT solvers, have been around for years. They are very powerful, but relatively tedious to use since they only know how to solve one problem: given a giant formula in first order logic (variables that can be either true or false, connected by AND and OR operators, with some negation operators sprinkled in), find an assignment of Boolean values to the variables in the formula such that the whole thing comes out as true. These tools can also determine that no such assignment exists and report that the input formula is unsatisfiable. I showed a little example of using these for solving Sudoku puzzles in a past post.

SMT solvers allow us to write down formulas that involve more than Boolean values and truth constraints: we can use integers and other richer mathematical structures (hence the word “theories” in the name). This is where we find a way to encode our Phish concert problem in a form that we can use a powerful SMT solver to tackle.

Encoding the problem

How do we go about encoding it? Fortunately, the encoding is relatively straightforward. Let’s consider for a moment what our goal is. We want to listen to every song at least once, but want to minimize the number of shows to do so. This means we have a few things to tell the solver:

• Encode the concept of listening to every song.
• Encode the concept of listening to a show 0 or 1 times.
• Encode the relation of shows to the songs that appear in their setlists.
• Encode constraints to guarantee every song is listened to in the solution.

The way I solved this was by setting up a set of integer constraints that the solver was given to solve. In this post, I make use of the Z3 solver from Microsoft Research. Z3 is an impressively powerful solver that was made free in the last few years, so it’s worth playing with. It’s available on every major computer OS and can be programmed from a number of languages. In this post, I use the Python bindings that it provides. My original version used the direct SMT-LIB encoding via s-expressions, but given that the audience is likely more familiar with Python I went with that here.

Data munging

To start, we need some data. Fortunately, the person who originally posed the problem on reddit wrote a scraper for Phish.net and put it up on GitHub. The data that was collected gave us the following:

• For each show, the collection of songs it contains.
• For each song, the collection of shows they occur in.

Furthermore, their data allows us to identify songs as originals versus covers: a useful dimension if one wants to hear every song that they performed by any artist, or restrict the solution to only Phish compositions.

The scraper doesn’t provide any additional information, so date, venue, city, and so on, must be inferred from the URLs that they recorded. I will admit: I haven’t played much with the Phish.net API for this task, so that is likely a cleaner way to go that will give the information that we need more directly. But for now, the scraped data is sufficient (and allowed me to work offline, avoiding wasting the bandwidth of the Phish.net site).

Encoding

Let’s start the process of encoding the problem as constraints for the solver. Before I start, one word of warning: you might say during the process “why didn’t you do X instead?”. The short answer: no real reason. Often there are multiple ways to express problems in the form of constraints. If you have ideas on a different encoding, perhaps this article will give you enough of a starting point to try it out! To be honest, I started my solution by treating the problem as a minimum constrained bipartite graph matching problem, so I think some of the constraints are from my first experiments with the encoding a couple years ago. Regardless, let’s move on to the encoding.

Before the encoding, we have to load up the data. The IO code isn’t included here since it’s primarily responsible for converting the CSV tables to Python data structures. There are three lists that are created: a list of show identifiers (e.g., ‘h123’), a list of song identifiers (e.g., ‘s42’), and a list of edges that relate shows and songs based on setlist inclusion (e.g., (‘h123’, ‘s42’) indicating that song s42 occurred in show h123).

The easiest place to start are the song and show inclusion constraints. This is where we establish the set of variables representing each song or show. We know we are going to be eventually counting shows and songs, so we probably want to use Integer variables instead of Booleans. To start, we declare the Z3 variables for each show and song. The IntVector constructor gives a compact way of creating a bunch of them all at once.

song_v = IntVector('s',len(songs))
show_v = IntVector('h',len(shows))

We are also going to need a way of cross referencing the Z3 variables with our song IDs, and vice versa. This is useful when Z3 finds a solution: we want to be able to map the solution back to the original data from the Z3 variables. There may be a cleaner way of doing this by encoding the song IDs directly in the Z3 variable API - I didn’t bother looking (the Z3 API docs for Python are… non-standard.) The quick and dirty way involved a few simple dictionaries:

song_vs = dict(zip(song_v, songs.keys()))
show_vs = dict(zip(show_v, shows.keys()))
song_sv = dict(zip(songs.keys(), song_v))
show_sv = dict(zip(shows.keys(), show_v))

The suffix “vs” indicates a mapping from Z3 variable to source, and “sv” maps from source to Z3 variable.

Once we have that, we want to include a constraint that indicates a song or show either is or is not included. We aren’t using Booleans, so the best we can do is to say the value for each show/song is either 0 or 1: or in the language of constraint logic, for each variable X, X >= 0 and X <= 1.

song_c1 = [And(song >= 0, song <= 1) for song in song_v]
show_c1 = [And(show >= 0, show <= 1) for show in show_v]

Then, for all song/show combinations, they must add up to at least one:

edges_c1 = [show_sv[show] + song_sv[song] >= 1 for (show, song) in edges]

The next constraint encodes our original goal: every song must be included.

song_c2 = [Sum(song_v) >= len(songs.keys())]

We can see from this constraint that, when combining it with the earlier constraint restricting songs to either being assigned 0 or 1, this implies that all songs must be assigned 1 for this to be satisfied.

Finally, we want to impose the constraint that each song must be covered by at least one show. This requires us to first build up a list of Z3 variables for every show a song occurs in, so we can use it in the constraint later.

songEdgeMap = {}
for song in song_v:
    songEdgeMap[song] = []
for (show,song) in edges:
    songEdgeMap[song_sv[song]].append(show_sv[show])

The constraint is then easy to state:

song_c3 = [2 <= (song + Sum(songEdgeMap[song])) for song in song_v]

At this point, we have defined the cover problem, but have one remaining constraint to add: the one that restricts the size of the cover. That’s important since we are attempting to minimize that. Constraining the problem to a specific cover size (or minimizing it) is what makes the set cover problem challenging. Just finding a set cover is pretty easy - just keep grabbing subsets until you cover the whole set. Say we want to ask if we can find a set of 71 or less shows that cover all songs. We can pose that this way:

show_c2 = [Sum(show_v) <= 71]

Solving the problem

Once we have this, we can hand the constraints off to Z3 to do the heavy lifting and see if an answer can be found. This entails instantiating the solver, adding the constraints, and asking if they can be satisfied:

s = Solver()
s.add(song_c1 + song_c2 + song_c3 + show_c1 + show_c2 + edges_c1)
if s.check() == sat:
    print("sat")
    m = s.model()
    for show in show_v:
        if m.evaluate(show).as_long() > 0:
            print(shows[show_vs[show]])
else:
    print("failed to solve")

In the event that the solver says they can be satisfied, we can then ask for the model it found and run through the set of variables looking for shows that are set to non-zero values. Once we have those, we can use the tables we created to map from variable objects back to the show data to figure out what shows it found for us.

In my initial code, I solved the optimization problem by iteratively reducing the number in the constraint show_c2 until the solver reported unsat. I have not used the Optimize class that Z3 provides which can do this for you (and perhaps do it more efficiently - I don’t know). It turns out the person who originally posed the problem on reddit found via a greedy solution that the answer was somewhere in the low 70s or high 60s, so I was able to start there and iteratively shrink the number until we hit unsat. Solving the same problem for the full song repertoire including covers was harder: in that case, I started with a number I knew was too few, and had the solver iteratively increase the song count until it found a satisfying solution.

Results

So what’s the answer? Working with the static data I found on github which spans October 23, 1984 to January 15, 2017, we can generate two answers. The minimum number of shows to see all Phish original songs over that period is 70 shows. The minimum number of shows to see all Phish originals plus covers over that same time period is 246 shows. In each case the solver took around 20-25 minutes to come up with a solution satisfying the constraints. That isn’t ideal, but to be honest, it didn’t seem that bad given that I put absolutely no effort into trying to speed it up (see notes below for some thoughts on that).

The show lists are provided below for those who are curious. I didn’t run the scraper found on GitHub to get a more up-to-date show list, which is unfortunate, since I think the Baker’s Dozen run from 2017 could have a big impact on the results (or not - without the data, who knows!). Aside from the fact that it appears the scraper violates the terms of use for the Phish.net data, I also couldn’t get it to rebuild (I don’t use eclipse, and the original author appeared to - so I ran out of patience trying to rebuild it myself). As we say in the academic world when we have an idea but have run out of time to do it - “Future work”.

Notes

Now, at this point a setlist geek like myself might say “wait, that’s not the full story” - and you’d be correct. Here are some of the obvious things to consider in the approach above.

• The solution presented makes no use of the full setlist data from authoritative sources like Phish.net. For example, you might want to make sure you include shows where a song is actually played to completion - it isn’t uncommon for a setlist to indicate that a song is not completed during a given show. Does it count if we found a cover that includes only an incomplete instance of a song? I’d say no.

• You might also want to add constraints to say that you want to include only instances of songs that are listed in the Jam charts to make sure that you’re not only getting all of the songs, but getting some well regarded versions.

• Perhaps you also want to make sure you minimize the occurrences of specific songs for one reason or another. For example, one “Ass Handed” is enough for me.

• All that the solver guarantees is that the solutions it finds are minimal! There is no reason to believe that they are unique though - so it is entirely possible that one can find another set of the same number of shows that also cover the repertoire. The only thing it guarantees is that you can’t find a smaller set. Trying to find another minimal cover is relatively straightforward and is simply a matter of adding more constraints: effectively you would add to the constraints described above one more contraint that basically says “and not this set of shows”. That is a common method used to get a SAT or SMT solver to enumerate a set of different solutions to a constraint set.

• There are ways you can use knowledge that you have up front to reduce the size of the problem that the solver needs to solve. The simplest approach would be preprocessing the data to include songs that only occur once ever (e.g., songs from Halloween shows that are only played that one time, never to be revisited). Those songs force certain shows to be in the ultimate list, and immediately bring all of the other songs with them - pruning the set of shows and songs that you need to consider in the minimization problem.

• You could do something similar by starting with the set of shows you’ve attended, and then seeking the minimal number of shows that you did NOT attend to listen to in order to cover the song catalog. You really can go wild with the different kinds of constraints you can impose to answer different types of queries.

Unfortunately, the compute time for running the solver, while far faster than a brute force approach, is not something one wants to do often. Especially behind the scenes of a web site with limited resources. So I don’t expect this kind of thing to ever be practical to add to the Phish.net stats that we all can look up for the shows we’ve attended or rated unless a cleverer solver/encoding can be written up that requires far less time.

The show lists

For the curious, here are the minimal covers that were found for the date range October 23, 1984 to January 15, 2017.