Simulation, Dynamics, and the FPU Problem
I recently wandered by Powell’s Technical Books (one of the many perks of working in Portland is having this nearby) and left with the book “The Genesis of Simulation in Dynamics: Pursuing the Fermi-Pasta-Ulam Problem”. I think it’s a pretty interesting book relative to others that I’ve picked up on dynamics and chaotic systems. The book revolves around one problem and follows its development since it was first posed in the 1950s as the field of dynamics unfolded around it. I figured I’d give a quick description of the problem that the book discusses here and possibly interest others to grab the book.
The model that the book discusses is known as the Fermi-Pasta-Ulam (or FPU) problem. It is quite simple. Consider a 1D string that is represented as a sequence of line segments connected at n vertices. The connections between vertices are basically springs that obey Hooke’s law. In the model, the focus is on the displacement of these vertices over time. For the case where all vertices are equally spaced, the string doesn’t move at all since it is in an equilibrium state. When they are not uniformly spaced, interesting things start happening.
This video shows the case where the vertices are displaced based on a sine wave.
(Note: the slowing and speeding up of the video is artificial and not part of the model, but is due to variations in compute time per frame on my computer since I recorded this as a screen capture).
The model is defined by tracking the second derivative of the position of the vertices. The unperturbed linear model is described as:
\[ \ddot{q}_j = (q_{j+1}-q_j) + (q_{j-1}-q_j) \]
Adding in a perturbation that is nonlinear is what introduces the interesting behavior:
\[ \ddot{q}_j = (q_{j+1}-q_j) + (q_{j-1}-q_j) + \alpha \left[(q_{j+1}-q_j)^2 - (q_j - q_{j-1})^2\right] \]
The parameter alpha allows us to control the amount that this nonlinear term contributes to the evolution of the system. In my example movies, I let alpha be somewhere around 0.5. In Matlab, this is easily written as:
function fpu(n,alpha,s,dt,iters)
% initial positions for n points on the line
% and two additional points for the fixed ends
q = (0:n+1)./(n+1);
qrest = (0:n+1)./(n+1);
% velocities start as zero
qvel = zeros(1,n+2);
% perturbation added with a sinusoid
q = q + 0.1.*sin(s.*q .* pi);
% make sure ends are fixed at 0 and 1
q(n+2) = 1; q(1) = 0;
for i=1:iters
% first term of q"
qterm1 = q(3:end)-q(2:end-1);
% second term of q"
qterm2 = q(1:end-2)-q(2:end-1);
% qacc is q". note that (a-b)^2 = (-(b-a))^2
qacc = qterm1 + qterm2 + alpha .* (qterm1.^2 - qterm2.^2);
% velocity is velocity + acc
qvel(2:end-1) = qvel(2:end-1) + qacc;
% position is updated by velocity * time step
q(2:end-1) = q(2:end-1) + qvel(2:end-1).*dt;
end
endAdding a few strategic plot commands at the end of that loop lets you visualize it and see the plot I showed above.
The goal of the model originally was to look at how the energy in the system moved between the different vibrational modes of the system. As can be seen pretty clearly in the video above, over time, the single low frequency sinusoid that the system starts with evolves into a more complex motion where higher frequency modes gain energy and contribute more to the state of the system.
We can look at the energy in each mode by writing the Hamiltonian of the system as:
\[ H_0(a,\dot{a}) = \frac{1}{2}\sum_{k=1}^n(\dot{a}_k^2 + \omega_k^2a_k^2) \]
where:
\[ \omega_k = 2 sin \left(\frac{k \pi}{2(n+1)}\right) \]
So, if we compute each component of the sum and look at them individually (instead of looking at the overall energy of the system represented by \(H_0\)), we can see how the different modes contribute to the overall energy of the system. The code above can be easily modified to add this computation after the update to the q vector:
for k=1:n
a(i,k) = (sqrt(2/(n+1))) * sum(q(2:end-1).*sin((1:n)*k*pi/(n+1)));
ap(i,k) = (sqrt(2/(n+1))) * ...
sum((j/n+1).*pi.*q(2:end-1).*cos((1:n)*k*pi/(n+1)));
end
h(i,:) = 0.5 .* (ap(i,:).^2 + omega.^2 .* a(i,:).^2);Here is a look at the energy of modes 2-8 for the first 30000 iterations of the Matlab code:
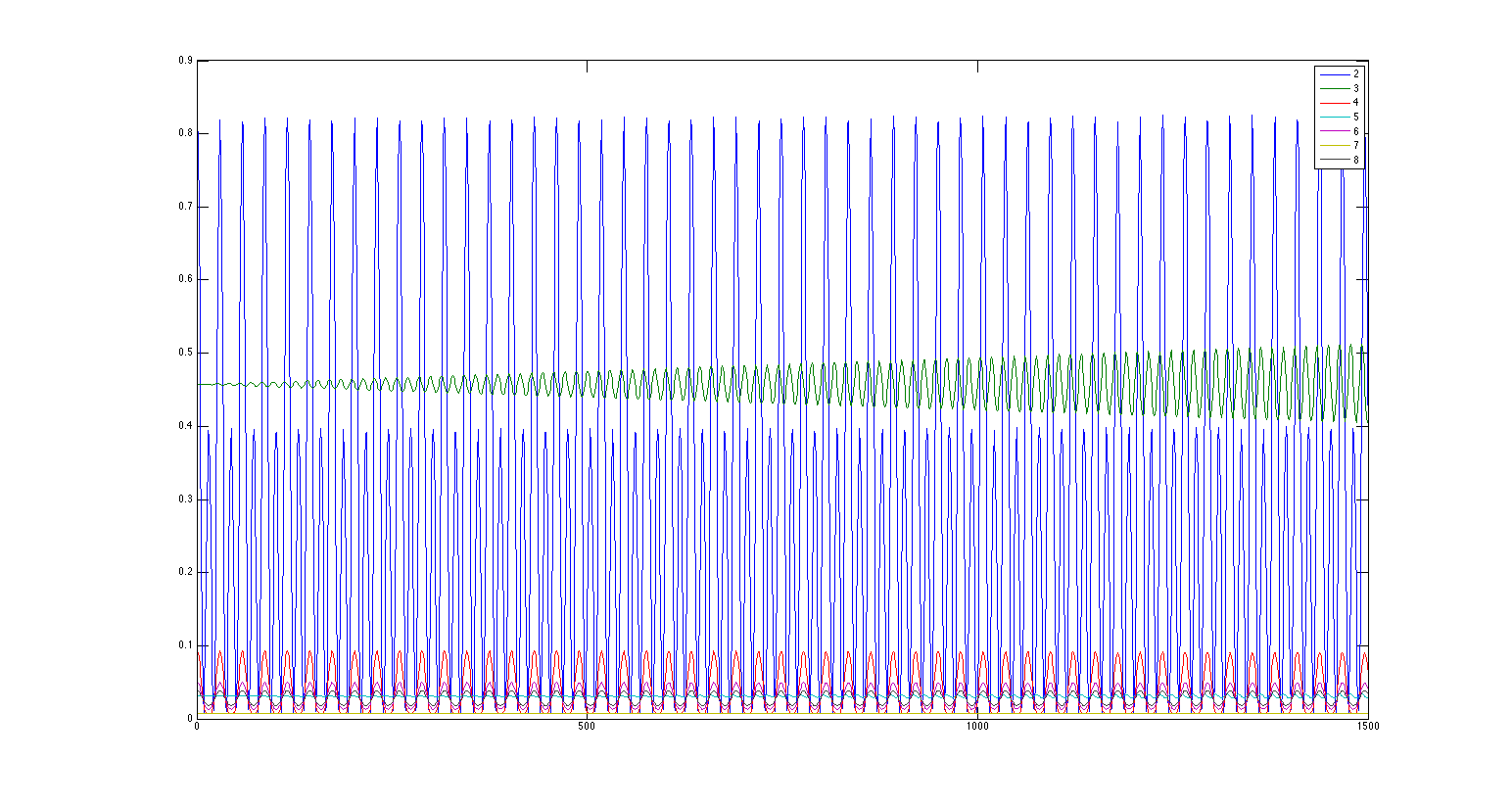
As we can see, over time some of the higher frequency modes begin to gain more energy. This is apparent in the video as well.
Just for fun, we can also look at an instance of the problem where we intentionally start off with a perturbation. In this case, we start off with initial conditions that cause the right-most link in the chain to be stretched further than the rest, leading to a wave that moves back and forth down the string. The impact of this on the energy distribution is interesting as well.
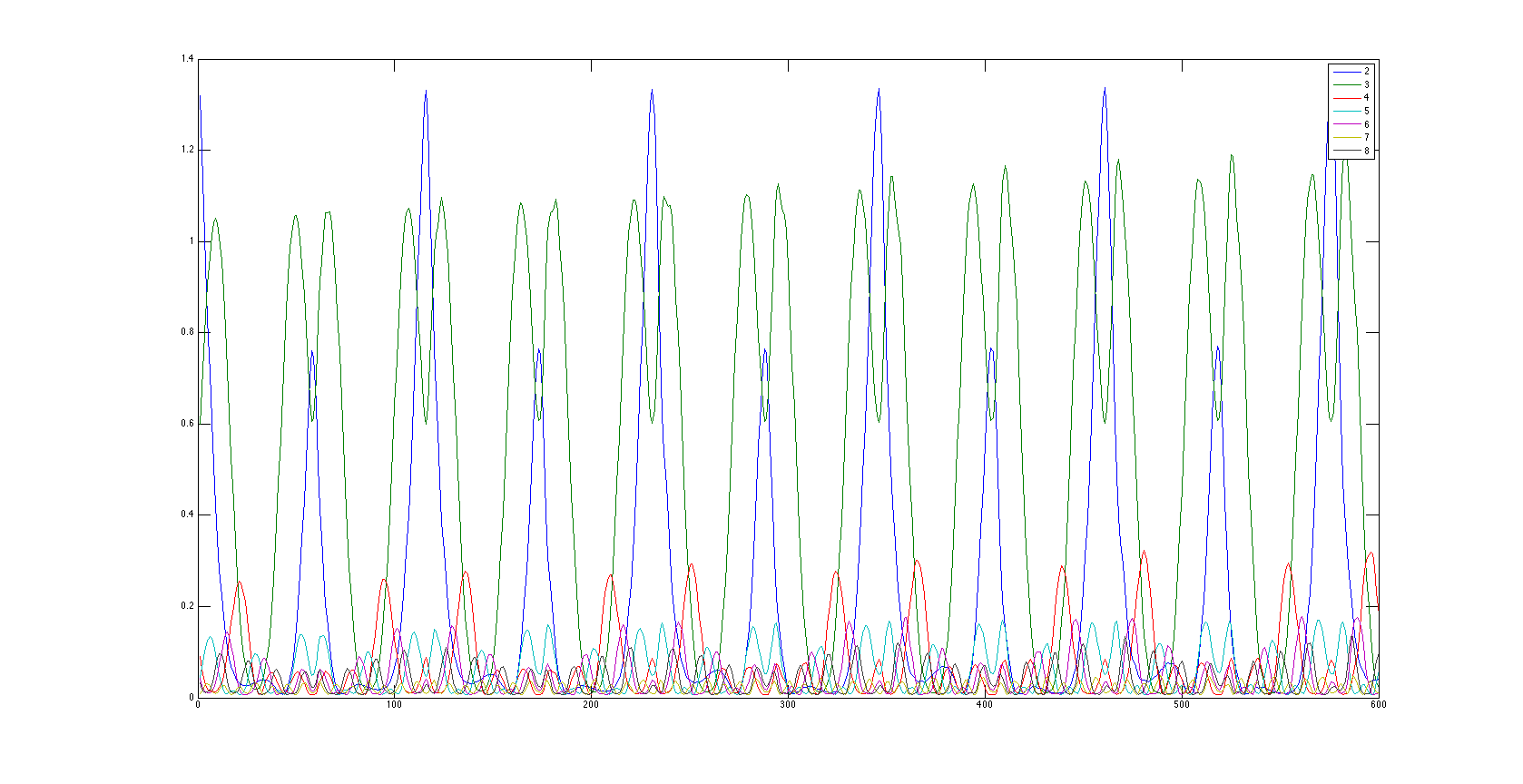
This video was created using the code above, but instead of passing a nice integer value for the parameter s (like 1.0), I passed in a value like s=1.3.
Looking at the plot of the energy in each mode, we see that now things are less regular. For example, look at the plot for mode 3 - instead of being a nice smooth peak, the shape of the peaks over time changes. This plot spans the first 3000 iterations of the model for this case, allowing us to look a bit more carefully at the behavior at a fine time scale.
Overall, I think this problem is an interesting one to play with and use to learn a little about dynamical systems. I’m not done with the book yet, but so far it is pretty interesting. Fortunately, these days we have computers far faster than those that Fermi and friends had, so it is possible to casually play with problems like this that were quite challenging to work on back in the earliest days of computing.