3D Diffusion limited aggregation in Haskell
I come from the scientific computing community where, historically, most of my coding was in languages like Fortran or C due to the ease by which one can create fast code. Simulations can run for a long time, so languages that emit high performance code are important. Even languages like Python and Matlab call out to routines written in these other compiled languages for computationally intensive routines where speed matters. Unfortunately, while Fortran and C are fast, they lack in comparison to their high level cousins in that they put you fairly close to the metal and abstractions are hard to capture in the code. The problem being solved ends up being convoluted and obfuscated in the translation from the domain formulation into code. Fortran is tolerable in some cases, especially when dealing with highly array-oriented code due to the presence of a rich array type that has existed in the language since the Fortran 90 standard (which, really, was borrowed from APL). This post examines a simulation that doesn’t have this nice array-oriented structure, and instead relies on tree-based data structures for rapidly querying a particle set based on spatial properties.
The language of choice for this post is Haskell. Why? A few reasons. The code described here actually started life as a C program, which I then translated to F#. The translation to F# was due to an interest I had in that emerging language, and the fact that I’m a native ML programmer. The move to Haskell from F# was undertaken since I was eager to learn Haskell, and I was curious to see how hard it is for a non-expert in the language (like myself) to generate code that performs well. In a followup post, I’ll discuss how it was possible to achieve performance only a couple times slower than C - close enough for it to be useful.
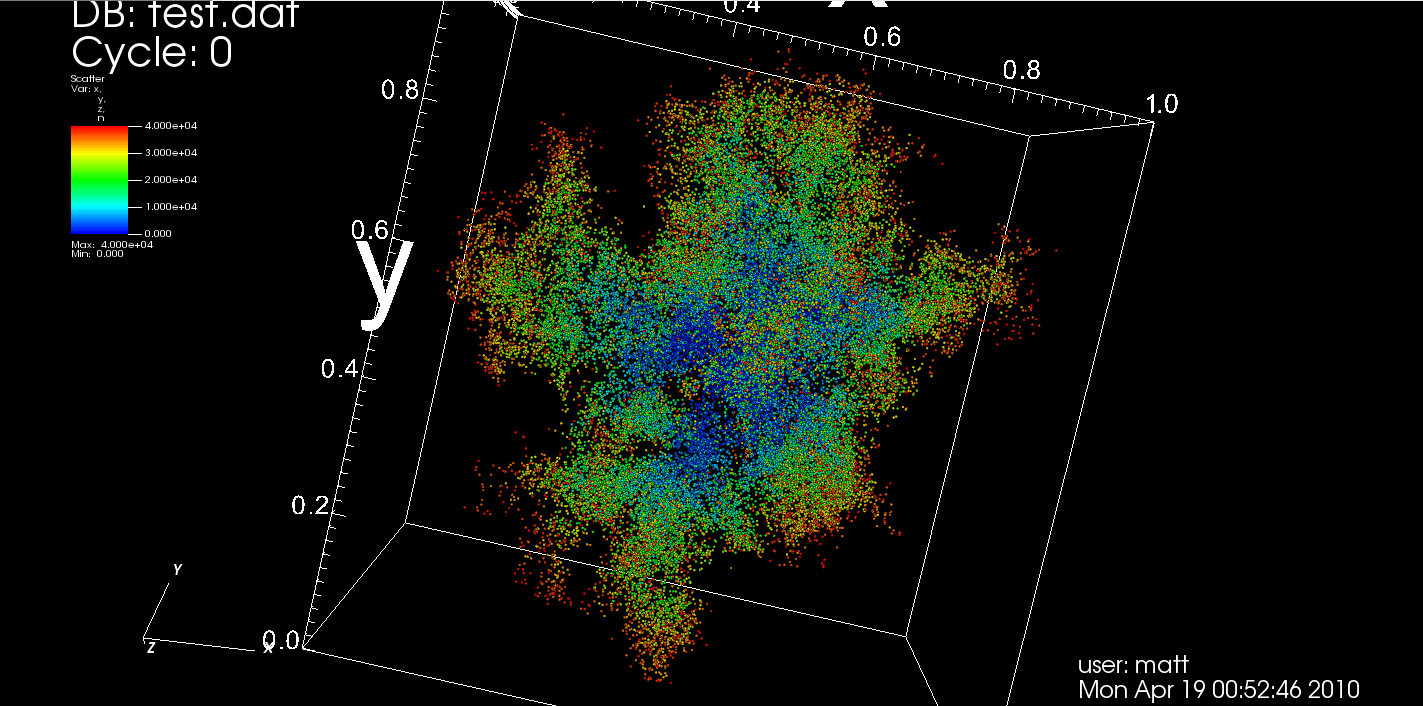
The model in question here is known as Diffusion-Limited Aggregation (DLA), and has existed in the physics literature for about three decades. A perusal of Physical Review E for that period of time shows articles on the model consistently popping up. Here is a picture of some output from the code for 40,000 particles that I describe in this post. The data produced by the code is a list of points as coordinates (x,y,z) and the order in which they were added to the growing structure. The visualization was performed using a rather nice tool for scientific visualization from Lawrence Livermore National Laboratory called VisIt. The color of each particle corresponds with the order in which it joined the aggregate (so the core is blue near 0, and the fringe is orange near 40,000).
I’ve also made a movie of a smaller aggregate that is on YouTube where you can see a full rotation of the structure. That visualization was generated using POVRay. I admit, I think I did something wrong in the process of taking the set of nice, crisp frames and making a movie to upload to YouTube. The video that is linked to here is a bit fuzzy and ugly, but the general point seems to be conveyed.
The basic algorithm for the DLA simulation described in this post is described below. It should be noted that this deviates a bit from some of the simpler versions of the model in the literature. A more common version of the algorithm assumes that the space is discretized as a grid in two or three dimensions, and the particle walk is confined to the grid itself. The model I describe doesn’t assume that the particles are confined to a grid, which leads to the slightly more difficult task of collision detection. Confinement to a grid makes collision detection really easy - just an array look up. Modeling space continuously instead of confining motion to a rectilinear grid seemed more appealing, although algorithmically more challenging.
We start with a single seed particle that resides at the origin. A new particle is created on the surface of a sphere of radius r centered on the origin. This particle then takes a random walk with a step size that is small relative to the radius of the sphere. As the particle walks around, we check to see if it comes within a predefined epsilon of the seed particle. This epsilon can be thought of as a function of the radius of the particle treated as a sphere instead of a point. If it does come within epsilon of some particle already in the structure that is growing, we perform a test to see if it sticks to the aggregate. This decision is governed by a “stickiness” parameter. If it passes, the particle becomes fixed and we repeat the process with a new particle, testing whether or not it wanders in and sticks to the set of particles that have joined the aggregate so far.
During this process, we need to make sure particles don’t wander too far away since they may never come back. This is accomplished by creating a second, larger sphere that surrounds the sphere where particles originate, and if a particle crosses it, we destroy it and start over with a new particle somewhere on the starting sphere. Similarly, as the aggregate grows outward, we can imagine that it will approach the sphere on which the particles originate. Therefore, as the aggregate grows, we make sure that these two spheres grow along with it to ensure a safe starting distance for all new particles.
The implementation of the algorithm requires a few basic pieces:
- A space partitioning data structure for efficient collision detection. We will use a kd-tree.
- Fast random number generation. Next to collision detection, generation of random numbers is a critical computation performed in the code due to the random walk that is performed.
- A simple set of routines for manipulating vectors in 3-space.
- The algorithm that walks a single particle inwards.
- Code for detecting particles that wander too far away.
- Code for updating the sphere of origin for new particles.
I won’t bother with the implementation of the vector library, as many people have written them or downloaded one that someone else wrote at one point or another. All that is required are basic vector arithmetic operations, like addition, subtraction, scaling by a scalar value, dot product, norm, and normalization.
The only routine of interest for our purposes is one for generating random points that lie on a sphere of radius r. The code for this is below:
randVec :: Double -> DLAMonad Vec3
randVec r = do
phi <- nextF (2.0 * pi) -- phi ranges from 0.0 to 2.0*pi
z' <- nextF (2.0 * r)
let z = z' - r -- z ranges from -r to r
theta <- return $ asin (z / r)
return $ Vec3 (r*(cos theta)*(cos phi)) (r*(cos theta)*(sin phi)) zThis function returns a vector in 3-space that is of length r originating from the origin (0,0,0). The return type is a consequence of how we deal with random numbers in the code. We use an instance of the State monad that is called the DLAMonad to weave our random number generator state through the code behind the scenes. This could be avoided if the random number state was threaded explicitly through the code as a parameter and return value, but that would make things messy to read and write. We also avoid using a global random number generator state since that would limit potential parallelization (a topic for another post - parallelizing DLA is somewhat subtle in order to maintain a physically meaningful model.)
The function nextF is provided by the DLAMonad, and returns a random Double that lies between 0.0 and the upper bound specified by the argument. This function is responsible for reading the current value maintained by the state monad, generating a new random value, and storing the modified random number generator state back in the state monad. This could be accomplished with explicit state passing, but I think the state monad used this way makes the code easier to follow.
The code for this monad is shown below.
import System.Random.Mersenne.Pure64
import Control.Monad.State.Strict
newtype Rmonad s a = S (State s a)
deriving (Monad)
-- | The DLAMonad is just a specific instance of the State monad where the
-- state is just the PureMT PRNG state.
type DLAMonad a = Rmonad PureMT a
-- | Generate a random number as a Double between 0.0 and the given upper
-- bound.
nextF :: Double -- ^ Upper bound.
-> Rmonad PureMT Double
nextF up = S $ do st <- get
let (x,st') = randomDouble st
put st'
return (x*up)
-- | Run function for the Rmonad.
runRmonad :: Rmonad PureMT a -> PureMT -> (a, PureMT)
runRmonad (S m) s = runState m sAs we can see, the code for nextF is fairly straightforward - get the state, sample the PRNG, put the new state back, and return the sampled random value scaled from [0,1] to [0,up]. The only other function that we provide is runRmonad, which is used to bootstrap a function that runs within the DLAMonad with an initial value for the PRNG state. We’ll see this invoked later when we describe the driver code for the simulation. Note that in a later post when showing how to tune the code to make it perform closer to the original C version that this Haskell code started from, the use of the state monad will be avoided and a specialized state monad will be used.
Another interesting property of this code is the use of Control.Monad.State.Strict. This was not something that I used in my original version of the code, and instead I used the non-strict state monad. The problem with this was that, under some circumstances I would experience crashes due to running out of memory. Why would this occur you might wonder? The cause was that laziness would result in a buildup of thunks as the particle took its random walk. An unlucky walk that took a long time to either hit the aggregate or wander into the death zone where the particle was purged would cause too many thunks to be generated, and the code would explode and crash. The strict version of the monad prevents these thunks from being stored, and instead forces each random number selected to be computed without laziness.
The next critical part of the code is the KD-Tree data structure. This allows the code to store all particles that have been added to the aggregate so far and search them based on their location. In the original code in C, I had written this using an octree. Geoff Hulette, a student that I worked with on the project last year, chose instead to use a KD-Tree. This ended up performing far better than my octree code, so we ended up using it. The octree version did not get ported through the F# and Haskell versions, so no code for it is discussed here.
The data type that represents the tree is as follows.
A KDTreeNode can be either empty, a leaf containing a single particle at a single coordinate, or an inner node with a particle at a coordinate and two children. Note that the KDTreeNode data type is parameterized with a generic type that resides with the coordinates. This is used to store data related to each particle along with their coordinates. This could be something simple like the particle number so we can track the accumulation of particles over time, or something more complex related to whatever it is one could be modeling with the program. In the example code I wrote to generate the visualizations above, it was just an Int representing the order in which particles joined the structure.
The functions for working with KDTrees are below.
kdtAddWithDepth :: (KDTreeNode a) -> Vec3 -> a -> Int -> (KDTreeNode a)
kdtAddWithDepth Empty pos dat _ = Leaf pos dat
kdtAddWithDepth (Leaf lpos ldat) pos dat d =
if (vecDimSelect pos d) < (vecDimSelect lpos d) then
Node (Leaf pos dat) lpos ldat Empty
else
Node Empty lpos ldat (Leaf pos dat)
kdtAddWithDepth (Node left npos ndata right) pos dat d =
if (vecDimSelect pos d) < (vecDimSelect npos d) then
Node (kdtAddWithDepth left pos dat (d+1)) npos ndata right
else
Node left npos ndata (kdtAddWithDepth right pos dat (d+1))
kdtAddPoint :: (KDTreeNode a) -> Vec3 -> a -> (KDTreeNode a)
kdtAddPoint t p d = kdtAddWithDepth t p d 0What is going on here? Adding a point is actually achieved with a function called kdtAddWithDepth, and kdtAddPoint calls that with an initial depth of zero. kdtAddPoint is a convenience function provided to avoid exposing this depth parameter to users of the code. The depth is used to select which component of the vector is partitioning the tree at each level. If we label the vector components as (x,y,z), then the 0th layer looks at x, 1st layer looks at y, 2nd layer looks at z, 3rd at x, and so on. The vecDimSelect function is provided by the Vec3 module to extract these components. The logic of the add function is pretty close to what we expect from any binary tree. There are three cases to worry about : adding to an empty tree, adding to a tree composed of just a leaf, and adding to a tree that has more than one element in it. In each case, the choice of which side to traverse is driven by the comparison of the depth-selected vector component.
Next, there are the functions for searching.
kdtInBounds p bMin bMax =
(vecLessThan p bMax) && (vecGreaterThan p bMin)
kdtRangeSearchRec :: (KDTreeNode a) -> Vec3 -> Vec3 -> Int -> [(Vec3,a)]
kdtRangeSearchRec Empty _ _ _ = []
kdtRangeSearchRec (Leaf lpos ldat) bMin bMax d =
if (vecDimSelect lpos d) > (vecDimSelect bMin d) &&
(vecDimSelect lpos d) < (vecDimSelect bMax d) &&
(kdtInBounds lpos bMin bMax) then [(lpos,ldat)]
else []
kdtRangeSearchRec (Node left npos ndata right) bMin bMax d =
if (vecDimSelect npos d) < (vecDimSelect bMin d) then
kdtRangeSearchRec right bMin bMax (d+1)
else
if (vecDimSelect npos d) > (vecDimSelect bMax d) then
kdtRangeSearchRec left bMin bMax (d+1)
else
if (kdtInBounds npos bMin bMax) then
(npos,ndata) : ((kdtRangeSearchRec right bMin bMax (d+1))++
(kdtRangeSearchRec left bMin bMax (d+1)))
else
(kdtRangeSearchRec right bMin bMax (d+1))++
(kdtRangeSearchRec left bMin bMax (d+1))
kdtRangeSearch :: (KDTreeNode a) -> Vec3 -> Vec3 -> [(Vec3,a)]
kdtRangeSearch t bMin bMax =
kdtRangeSearchRec t bMin bMax 0The KDTree is intended to provide a space-oriented search capability. Given a region of three dimensional space, the data structure should be able to return all points that are in the tree that fall within that region. The kdtRangeSearch function provides this. Like the function to add a point, the traversal requires knowledge of the depth at each level to decide which components of the range vectors are used for comparison. So, the kdtRangeSearch function hands control off to the actual search function with an initial depth of 0. As the kdtRangeSearchRec function traverses the tree, each point that is in the tree that falls within the bounding box defined by bMin and bMax are added to a list and returned. The result will be a list of points and their associated data. The order is meaningless within this list.
The final function of interest is that which, given a point not in the tree, determines if a collision will occur with any point already in the tree. This is the critical function called as particles take their random walk to potentially join the aggregate. Needless to say, it gets called quite frequently.
singleCollision :: Vec3 -> Vec3 -> Vec3 -> Double -> a -> Maybe (Vec3,a)
singleCollision pt start a eps dat =
if (sqrd_dist < eps*eps)
then Just (vecAdd start p, dat)
else Nothing
where
b = vecSub pt start
xhat = (vecDot a b) / (vecDot a a)
p = vecScale a xhat
e = vecSub p b
sqrd_dist = vecDot e e
kdtCollisionDetect :: (KDTreeNode a) -> Vec3 -> Vec3 -> Double ->
[(Vec3,a)]
kdtCollisionDetect root start end eps =
map fromJust $ filter (\i -> isJust i) colls
where
Vec3 sx sy sz = start
Vec3 ex ey ez = end
rmin = Vec3 ((min sx ex)-eps) ((min sy ey)-eps) ((min sz ez)-eps)
rmax = Vec3 ((max sx ex)+eps) ((max sy ey)+eps) ((max sz ez)+eps)
pts = kdtRangeSearch root rmin rmax
a = vecSub end start
colls = map (\(pt,dat) -> (singleCollision pt start a eps dat)) ptsThe function kdtCollisionDetect takes four arguments. First is the KDTree holding the particles to check a collision against. The second parameter is the starting position of the particle that is possibly colliding with the aggregate, and the third parameter is the position that particle would be at if it took a step and did NOT collide. The final parameter is the distance between particles that we consider to be sufficient for a collision to occur. As mentioned earlier, the particles in this model are considered not to be point particles, but tiny spheres. The coordinates simply indicate the center of the sphere. Epsilon should be considered to be twice the radius of the spheres - if two spheres have centers separated by epsilon or less distance units, then they have collided. Note that for this example we are not concerned with particles getting closer than epsilon – we allow them to overlap.
The first step in collision detection is to determine the region of space where we want to see if a particle already exists in the tree. The rmin and rmax computations determine these bounds by defining the corners of the cube based on the start and end position of the moving particle. The range search function is then invoked to check this space. The variable a is computed to represent the position of the particle within this range where we move the origin to the starting position of the particle - it just helps establish a relative coordinate system for the computation. We then map the function singleCollision over all potential collision candidates in the range to find all particles that we may have collided with. The contents of the singleCollision routine are basically a small bit of linear algebra to check each of these candidates to see if they are within epsilon of the particle being checked. The return value is the list of checked candidates that did actually fall within epsilon of the particle.
Up to this point, we have all of the machinery to implement the core of the simulation. We can walk particles around along their random walk, we can store them as they join the aggregate, and we can perform collision detection to decide whether or not a new particle gets added. This core is implemented in the function to walk a single particle around to either collide or wander outside the sphere in which we are working.
--
-- walk a single particle
--
walk_particle :: DLAParams -> Vec3 -> DLANode -> Int
-> DLAMonad (Maybe (DLAParams, DLANode))
walk_particle params pos kdt n = do
-- 1\. generate a random vector of length step_size
step <- randVec (step_size params)
-- 2\. walk current position to new position using step
pos' <- return $ vecAdd pos step
-- 3\. compute norm of new position (used to see if it wandered too far)
distance <- return $ vecNorm pos'
-- 4\. check if the move from pos to pos' will collide with any known
-- particles already part of the aggregate
collide <- return $ kdtCollisionDetect kdt pos pos' (epsilon params)
-- 5\. sample to see if it sticks
doesStick <- sticks params
-- 6\. termination test : did we collide with one or more members of the
-- aggregate, and if so, did we stick?
termTest <- return $ (length collide) > 0 && doesStick
-- 7\. have we walked into the death zone?
deathTest <- return (distance > (death_rad params))
-- check termination test
case termTest of
-- yes! so return the updated parameters and the kdtree with the
-- new particle added.
True -> return $ Just (update_params params pos',
kdtAddPoints [(pos',n)] kdt)
-- no termination... check death test
False -> case deathTest of
-- wandered into the zone of no return. toss the particle,
-- return nothing and let the caller restart a new one.
True -> return Nothing
-- still good, keep walking
False -> walk_particle params pos' kdt nA single step of this algorithm first samples the random number generator to take a step in some direction by step_size units. We compute where this particle would end up by adding the step vector to the position vector where the particle currently resides. The distance of this new position from the origin is computed so that it can be checked if it has wandered too far and must be destroyed. Next, the collision detection routine is called to determine if the particle collided with the existing aggregate. In the event that it does, the stickiness parameter is used to see whether or not it sticks or continues walking. Two tests are performed to check if it did collide and did stick, or if it walked too far away and needed to be purged. The case at the end of the function checks these tests, first to see if the particle stuck (in which case it is added to the aggregate), and if it did not stick, whether or not it was too far away. If it was, Nothing is returned. Otherwise, the function is recursively called with the new position that the particle walked to and the process repeats.
Overall, the structure of the code is satisfying in that the logic of the DLA model is fairly accurately captured without much obfuscation. The use of the Maybe type is employed to allow the caller to easily determine the outcome of the walk - if a particle did stick, then the return value is the new set of parameters and the KDTree with the new particle added. If it did not stick and walked too far away, the function returns Nothing. Notice that when a particle does stick, we return two items. As the aggregate grows, we may find that it is approaching the size of the sphere on which particles originate. We must keep this sphere sufficiently far from the aggregate to allow particles to walk inwards as if they originated far away. As such, when a particle joins the aggregate, we update the simulation parameters to allow the sphere of origin (and, correspondingly, the sphere where particles die) to grow.
Much of the remaining code, such as the main function or code to load parameter files off of disk, isn’t of much interest for the post. I do provide it all for download from my publicstuff GitHub repository, so feel free to check the code out if you’re interested in messing with the code.
What now? In a post in the not so distant future, I’m going to post the results of sitting down with some Haskell experts to tune the code to achieve performance comparable to the C version. One of the results of this tuning activity was the monad-mersenne-random package added to Hackage, which resulted from noticing that the pattern of using a state monad to thread PRNG state through the code is likely to be common in codes like this. What will be interesting will be looking at what lengths are required for different performance gains. It should be noted that the C code (also posted online in the publicstuff repo for the curious) was not highly tuned. So, to be fair, the Haskell code tuning will include discussion of “low hanging fruit” that can be learned by regular Haskell programmers, and some finer tuning that is beyond the likely scope of knowledge for a regular Haskell programmer. I personally don’t think it’s fair to present highly tuned code as representative of a language – the best representative of a language is the code that someone who has read the educational materials on the language would write. If those materials lead to poorly performing code, then it obviates the need for better educational materials.
What are my thoughts on the code presented in this post? First, I like it. One thing that I do find highly attractive about Haskell is the brevity of the code. Even the DLAMonad, which admittedly took a little while to figure out how to build, eliminates annoying explicit threading of state through parameters, making function signatures a bit cleaner. The use of the Maybe types in strategic places also is appealing, and reflects a similar pattern that I commonly employ in ML code based on the option type. I have to admit, I found laziness to be a significant burden here. There is no advantage to laziness that I can see in this particular program. If anything, it got in the way and caused bugs that required me to consult some local Haskell experts to find a solution to — which ultimately boiled down to purging laziness in critical parts of the program.
Stick around if you’re curious about how we tuned this code to go fast! Or, wait a little bit and I’ll talk about another interesting little code that I’ve been working with.